久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 曲線是平面內到定點的距離與到定直線的距離的距離之和為的動點的軌跡，則曲線與軸的交點的橫坐標是_____；又已知(為參數)，那么的最小值______．

答案，

．

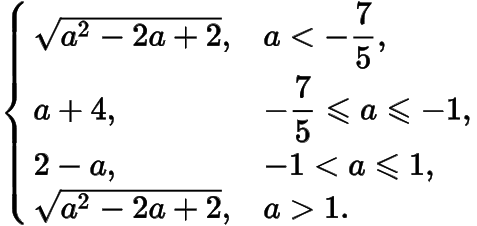
分析與解作與直線的距離為的兩條直線，，那么“到定點與定直線的距離之和為”，就轉化成了“在直線的左側到定點的距離與到直線的距離相等，或在直線的右側到定點的距離與到直線的距離相等”，如圖．

曲線由拋物線弧

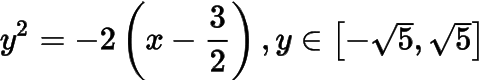
和拋物線弧

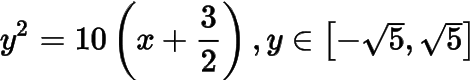
共同組成．

容易求出曲線與軸的交點坐標為．

接下來研究對于，的最小值．

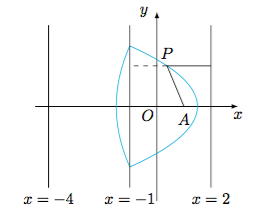
如下圖，設直線與直線，拋物線弧

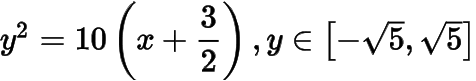
，直線，拋物線弧

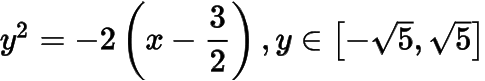
，直線依次交于，

，，，．

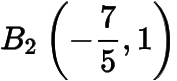
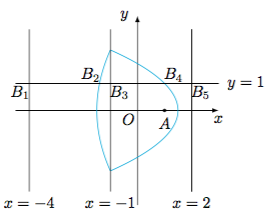
以為分界點分類討論：

當點位于的左側或的右側（即“鐘形”外部）時，的最小值為，當點為線段與曲線的交點時取到最小值；

當點位于之間時，若點在左側拋物線弧上，則有其中表示點到的距離；若點在右側拋物線弧上，則有其中表示點到的距離，等號都能取到．再比較與的大小即可得

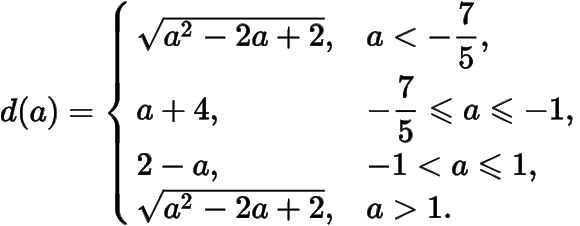
思考與總結本題是拋物線描述：“到定點與定直線距離之差為定值”的升級版本，需要補充輔助線．解決問題的關鍵是利用拋物線的定義將到定點的距離轉化為到定直線的距離．