(2010年廣東卷)設,是平面直角坐標系上的兩點,現定義由點到點的折線距離.對于平面上給定的不同兩點,.
(1) 若是平面上的點,試證明;
(2) 在平面上是否存在點同時滿足:和.若存在,請求出所有符合條件的點;若不存在,請說明理由.

分析與解(1) 根據題意,有

因此原命題得證.
(2) 第(1)小題中的不等式取得等號的條件是

即
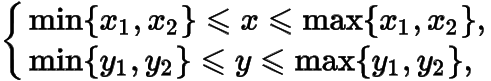
因此當或時,為的中點
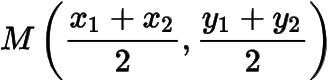
;當且時,點的軌跡是過的中點,斜率的絕對值為,且與直線斜率的符號相反的直線被以線段為對角線各邊都與坐標軸方向平行的矩形所截的線段,如圖所示.
注對于條件,即因為符號相關,的符號也相反,所以點的軌跡是斜率為或的直線.
若直線的斜率為正,不妨設,則有即點在斜率為的直線上,其它情況可同理.
思考與總結本題中的可以看成是折線段的定義,可以看成是折線垂直平分線的定義.類似的,我們可以定義折線圓,折線橢圓,折線雙曲線,點到直線的折線距離
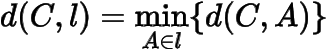
,以及折線拋物線.
