久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 　2011年廣東卷高考數學理科第21題（壓軸題）：

在平面直角坐標系上，給定拋物線

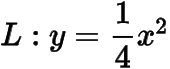
．實數滿足，是方程的兩根，記．

(1) 過點

()作的切線交軸于點．證明：對線段上的任一點，有

；

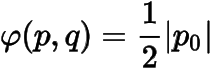
(2) 設是定點，其中滿足，．過作的兩條切線，切點分別為

，

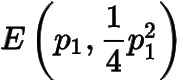
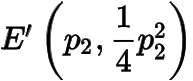
，與軸分別交于．線段上異于兩端點的點集記為．證明：

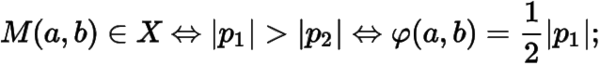
(3) 記

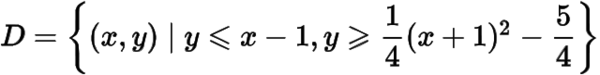
，當取遍時，求的最小值(記為)和最大值(記為)．

分析與解(1)法一顯然

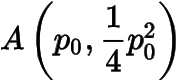
在拋物線上，于是過點的拋物線的切線方程為

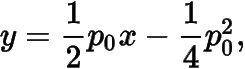
若，則線段的方程為

若，則線段的方程為

又若，則方程的兩根為

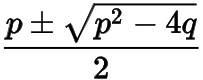
，若在線段上，則

從而，從而兩根為

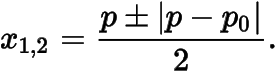
當時，，則

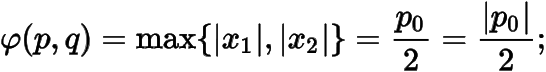
當時，，則

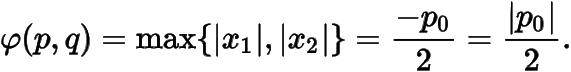
因此原命題得證．

法二過點的拋物線的切線方程為

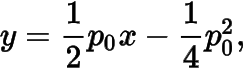
于是有

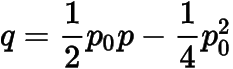
，從而考慮方程

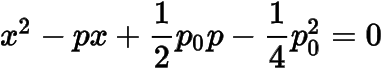
的兩根即可．

記方程左邊為，則有

所以方程的一根為

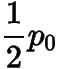
，另一根

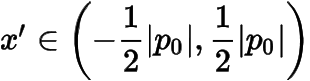
，從而知

．

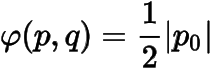
(2) 由題意知的方程分別為

聯立解得點的坐標為

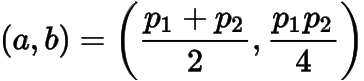
．從而考慮方程

它的兩根為

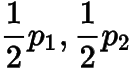
，所以

．

由此知等價于

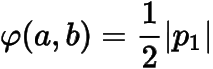
．下面證明當與它們等價：

由(1)知時，

；

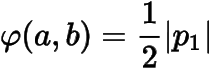
若，有

從而有．

(3) 如圖，表示直線與拋物線

所圍成的封閉區域(包含邊界)，其中，是直線與拋物線的兩個交點．

當點時，有

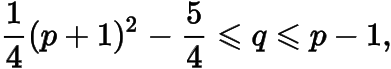
從而其中．于是有

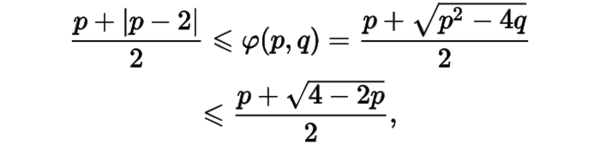
從而

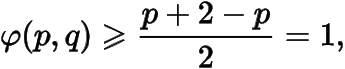
因此．

設，其中，則

所以

．

綜上所述，且