已知橢圓
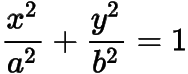
()的離心率
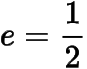
,過焦點(diǎn)且垂直于軸的直線被橢圓截得的線段長為.
(1) 求橢圓的方程;
(2) 斜率為的動直線與橢圓交于兩點(diǎn),在平面上是否存在定點(diǎn),使得當(dāng)直線與直線的斜率均存在時(shí),斜率之和是與無關(guān)的常數(shù)?若存在,求出所有滿足條件的定點(diǎn)的坐標(biāo);若不存在,請說明理由.
分析與解(1) 根據(jù)題意,通徑長
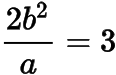
,于是橢圓的方程為
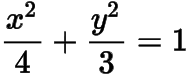
.
(2) 法一 仿射變換
利用仿射變換.設(shè)定點(diǎn)的坐標(biāo)為,平移坐標(biāo)系,使點(diǎn)為坐標(biāo)原點(diǎn),則橢圓方程變?yōu)?/p>
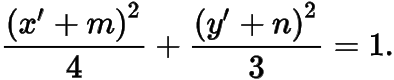
當(dāng)不過點(diǎn)時(shí),設(shè)動直線的方程為,則聯(lián)立直線與橢圓方程,有
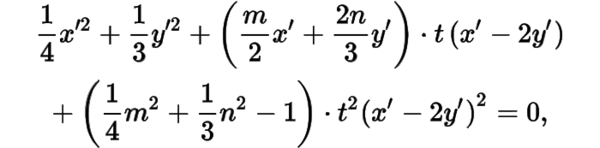
整理得的系數(shù)為
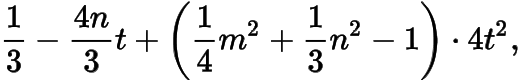
而的系數(shù)為
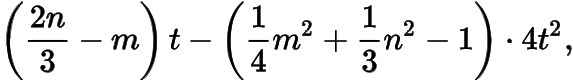
根據(jù)題意,直線與直線的斜率之和
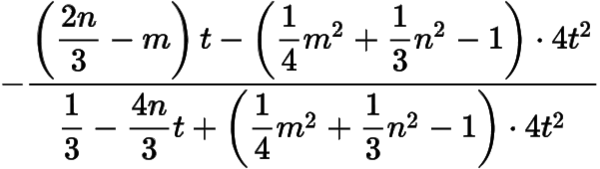
為定值.于是
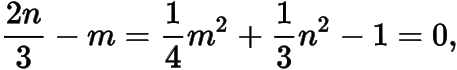
解得,
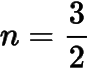
或,
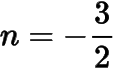
.對應(yīng)的點(diǎn)在橢圓上,于是不需要考慮過點(diǎn)的情形.
綜上所述,所有滿足條件的定點(diǎn)的坐標(biāo)為
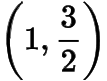
或
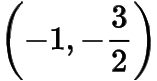
.
注可以將橢圓仿射為圓,則直線的斜率為
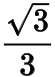
,于是點(diǎn)始終平分弧,進(jìn)而可取,此時(shí),因此直線與直線的斜率始終互為相反數(shù),符合題意.
法二 直接計(jì)算
設(shè)
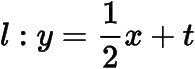
,與橢圓方程聯(lián)立得設(shè)
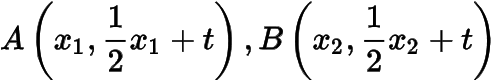
,則有直線的斜率之和
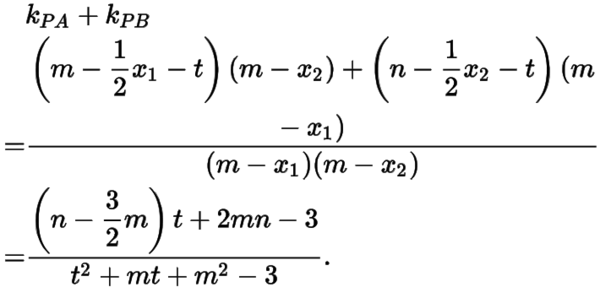
當(dāng)
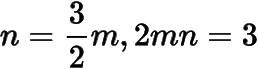
時(shí)斜率的和恒為,解得
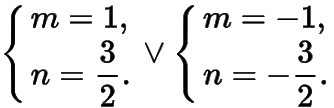
綜上所述,所有滿足條件的定點(diǎn)的坐標(biāo)為
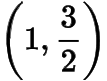
或
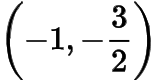

用戶可通過掃描二維碼實(shí)現(xiàn)移動客戶端訪問本站!
版權(quán)所有:中教未來(北京)文化傳播有限公司 Copyright(c)2001-2025 rights reserved www.3848080.com 京ICP備14025495號-5
高校特色專業(yè)招生咨詢熱線:4007-567-088
