久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 　極化恒等式設是兩個平面向量，則成立恒等式

有時也將上式寫成

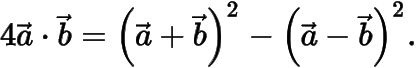
例已知是圓上的兩個點，是線段上的動點，當的面積最大時，則

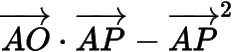
的最大值是______．

——提問者：風行者 2016-08-03 11:01

分析注意到

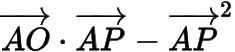
可變形為，因此，可嘗試利用極化恒等式進行思考．

解（答題者：意琦行）

設，結合，則

因此，當，即時，面積最大．所以

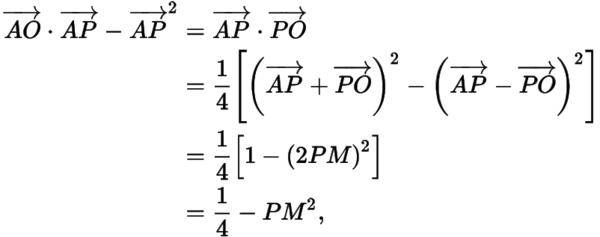
其中為的中點，如圖：

此時的最小值為

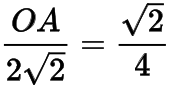
，故所求最大值為

．

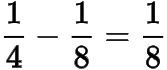
總結極化恒等式的主要作用在于，它可以將兩向量的數量積轉化為這兩個向量的“和向量”與“差向量”，因此，當兩個向量的“和向量”或“差向量”為定向量時，常常可以考慮利用極化恒等式進行轉化求解．

練習

1．如圖放置的正方形，，分別在軸、軸的正半軸（含原點）上滑動，則的最大值為______．

——提問者：風行者 2016-09-09 10:10

2．在等腰直角三角形 中，，點 為斜邊 的中點，點 在線段 上運動，則

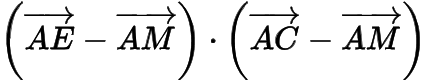
的取值范圍是( )

A．

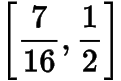
B．

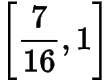
C．

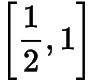
D．

——提問者：了然無聲 2016-10-13 11:53

3．如圖，在中，是的中點，是上的兩個三等分點，，，則的值是______．

——提問者：weilew 2016-08-24 11:43

答案

1．；

2．A；

3．．

備注：若要查閱詳細的解答過程，請在光子問答APP中搜索用戶名，查看用戶提問的問題，找到對應時間所發的題即可．