08：00-24:00
(2013年海淀高三期末)已知正方體的棱長為，動(dòng)點(diǎn)在正方體表面上運(yùn)動(dòng)，且()．記點(diǎn)的軌跡的長度為．
(1) 求
；
(2) 求出關(guān)于的方程的解的個(gè)數(shù)的所有可能的值，并說明理由．
分析與解由于正方體繞其體對(duì)角線旋轉(zhuǎn)后仍與自身重合，于是為點(diǎn)在正方體的側(cè)面與上的軌跡長度之和的倍．將右側(cè)面翻折至與側(cè)面重合，如圖．稍加探索可以發(fā)現(xiàn)和是兩個(gè)分界點(diǎn)．
(1) 當(dāng)時(shí)，有
，于是
．
(2) 當(dāng)時(shí)，圖中弧的半徑為，所對(duì)的圓心角為
記
，其中
，則對(duì)應(yīng)的弧長
其導(dǎo)函數(shù)
于是隨著的增大，隨之增大，對(duì)應(yīng)的弧長隨之減小，隨之減小．
當(dāng)時(shí)，設(shè)
，其中
，則弧長之和
于是
設(shè)
則
，
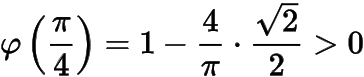
，而
因此在
上先負(fù)后正，對(duì)應(yīng)的在
先遞減再遞增．
這樣我們就可以勾勒出函數(shù)的圖象如下．
于是方程的解的個(gè)數(shù)的所有可能值為．
注本題是北京海淀區(qū)高三期末考試的一道填空題，為了嚴(yán)格地說清為什么解的個(gè)數(shù)有且只有這些很需要費(fèi)一番功夫．
根據(jù)學(xué)生的高考分?jǐn)?shù)、意向?qū)I(yè) 為您查找適合你的院校列表， 24小時(shí)內(nèi)短信電話發(fā)送給你！
用戶可通過掃描二維碼實(shí)現(xiàn)移動(dòng)客戶端訪問本站！
版權(quán)所有：中教未來（北京）文化傳播有限公司 Copyright(c)2001-2025 rights reserved www.3848080.com 京ICP備14025495號(hào)-5
高校特色專業(yè)招生咨詢熱線：4007-567-088
