久久亚洲国产精品_久久精品在线免费观看_国产成人精品a视频一区www_在线播放精品

 感謝關(guān)注（笑臉）如您尚未關(guān)注，請點擊上方藍字“高考”關(guān)注我們或識別文末二維碼，獲取更多知識方法。每日更新，與您不見不散！

解決等差數(shù)列與等比數(shù)列的綜合問題，關(guān)鍵是理清兩個數(shù)列的關(guān)系。如果同一數(shù)列中部分項成等差數(shù)列，部分項成等比數(shù)列，要把成等差數(shù)列或等比數(shù)列的項抽出來單獨研究。

如果兩個數(shù)列通過運算綜合在一起，要從分析運算入手，把兩個數(shù)列分割開，弄清兩個數(shù)列各自的特征，再進行求解。

對等差、等比數(shù)列的概念、性質(zhì)要有深刻的理解，有些數(shù)列題目條件已指明是等差(或等比)數(shù)列，有的數(shù)列并沒有指明，但可以通過分析構(gòu)造，轉(zhuǎn)化為等差數(shù)列或等比數(shù)列，然后應(yīng)用等差、等比數(shù)列的相關(guān)知識解決問題。

數(shù)列是一種特殊的函數(shù)，故數(shù)列有著許多函數(shù)的性質(zhì)。等差數(shù)列和等比數(shù)列是兩種最基本、最常見的數(shù)列，它們是研究數(shù)列性質(zhì)的基礎(chǔ)，與函數(shù)、方程、不等式、三角等內(nèi)容有著廣泛的聯(lián)系，在實際生活中也有著廣泛的應(yīng)用，隨著高考對能力要求的進一步提高，這一部分內(nèi)容也將受到越來越多的關(guān)注。

一、數(shù)列在實際生活中有著廣泛的應(yīng)用，其解題的基本步驟，可用圖表示如下：

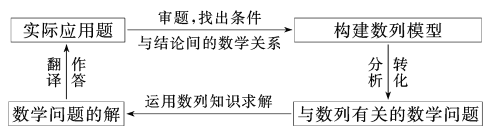
典型例題1：

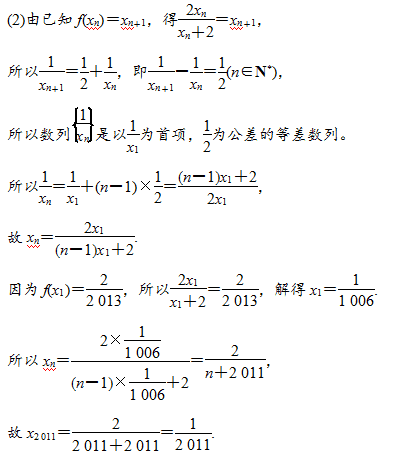
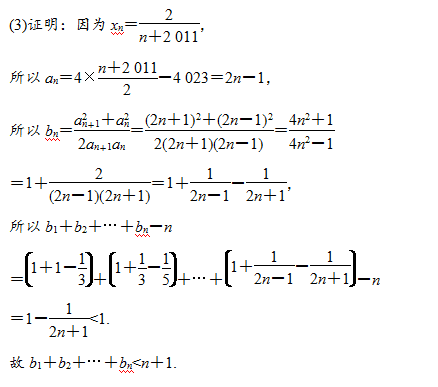
二、數(shù)列應(yīng)用題常見模型

1、等差模型：如果增加(或減少)的量是一個固定量時，該模型是等差模型，增加(或減少)的量就是公差。

2、等比模型：如果后一個量與前一個量的比是一個固定的數(shù)時，該模型是等比模型，這個固定的數(shù)就是公比。

2、遞推數(shù)列模型：如果題目中給出的前后兩項之間的關(guān)系不固定，隨項的變化而變化時，應(yīng)考慮是an與an＋1的遞推關(guān)系，還是前n項和Sn與Sn＋1之間的遞推關(guān)系。

典型例題2：

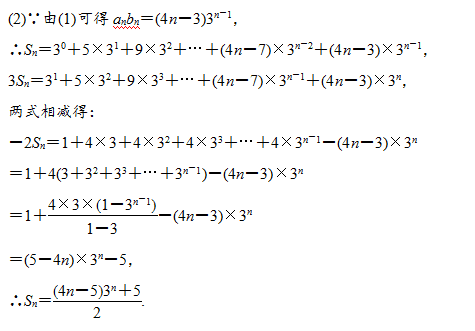
三、數(shù)列實際應(yīng)用題的解題策略

解等差、等比數(shù)列應(yīng)用題時，首先要認真審題，深刻理解問題的實際背景，理清蘊含在語言中的數(shù)學(xué)關(guān)系，把應(yīng)用問題抽象為數(shù)學(xué)中的等差、等比數(shù)列問題，然后求解。

四、處理分期付款問題的注意事項

1、準確計算出在貸款全部付清時，各期所付款額及利息(注：最后一次付款沒有利息)。

2、明確各期所付的款以及各期所付款到最后一次付款時所生的利息之和等于商品售價及從購買到最后一次付款時的利息之和，只有掌握了這一點，才可以順利建立等量關(guān)系。

典型例題3：

五、數(shù)列與函數(shù)的綜合問題主要有以下兩類：

1、已知函數(shù)條件，解決數(shù)列問題，此類問題一般利用函數(shù)的性質(zhì)、圖象研究數(shù)列問題；

2、已知數(shù)列條件，解決函數(shù)問題，解決此類問題一般要充分利用數(shù)列的范圍、公式、求和方法對式子化簡變形。

另外，解題時要注意數(shù)列與函數(shù)的內(nèi)在聯(lián)系，靈活運用函數(shù)的思想方法求解，在問題的求解過程中往往會遇到遞推數(shù)列，因此掌握遞推數(shù)列的常見解法有助于該類問題的解決。

本文來源于吳國平，圖：互聯(lián)網(wǎng)，如有轉(zhuǎn)載，請聯(lián)系并注明原出處。如果喜歡可以分享這篇文章到朋友圈！