2012年新課標 I 卷理科數學第21題:
已知函數滿足

.
(1) 求的解析式及單調區間;
(2) 若
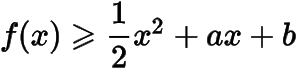
,求的最大值.
分析與解(1) 根據題意,函數的導函數分別令和,可得
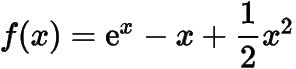
.進而其導函數于是函數的單調遞增區間是,單調遞減區間是.
(2) 根據題意,有取函數的斜率為的切線,設切點為,則切線方程為其中.易知等號當且僅當時取得.因此.由于,于是記右側函數為,則其導函數于是當
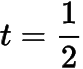
時,取得極大值,亦為最大值.于是的最大值為,此時,
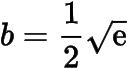
.
思考與總結從圖形的角度看待題中的不等式,將含有兩個變元的式子轉化為只含一個變元的式子.
下面給出一道練習:
練習已知,且.若在的定義域內恒有,求的最大值.
答案

.
提示時不等式顯然不會恒成立,只考慮,此時有

等號當且僅當
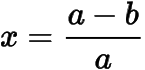
時取到,從而得到,有右邊的式子的最大值為

